Giới thiệu về hình thoi
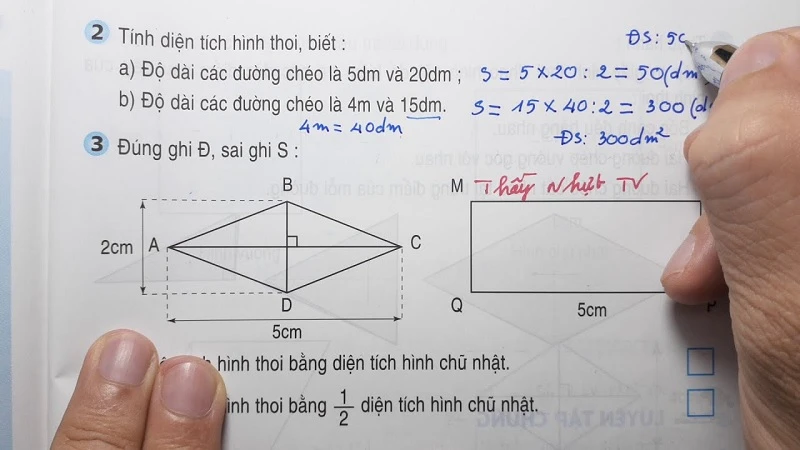
Hình thoi là một trong những hình học cơ bản, có nhiều ứng dụng trong thực tế. Đặc điểm nổi bật của hình thoi là cả bốn cạnh đều có độ dài bằng nhau và các góc đối diện bằng nhau. Hình thoi cũng có hai đường chéo cắt nhau tại trung điểm và vuông góc với nhau. Việc tính toán các thông số như diện tích, chu vi hay độ dài đường chéo là rất quan trọng khi làm việc với hình thoi. Trong bài viết này, chúng ta sẽ khám phá cách tính độ dài của hai đường chéo của hình thoi thông qua các công thức cụ thể.
Đặc điểm của hình thoi và đường chéo
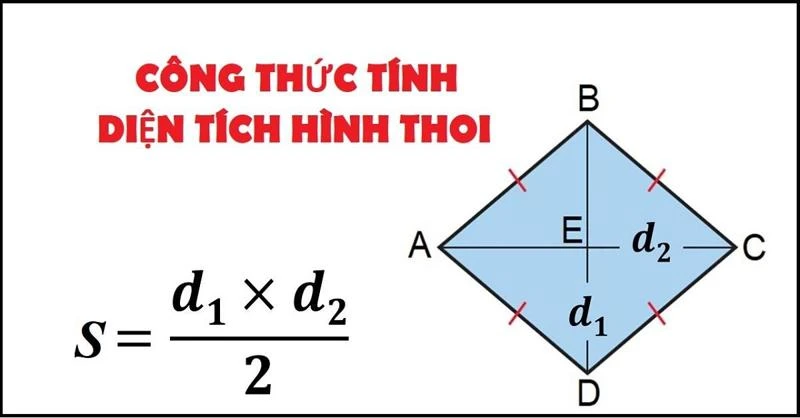
Trước khi đi vào cách tính, chúng ta cần hiểu rõ về các đặc điểm của hình thoi. Các đường chéo của hình thoi được ký hiệu là d1 và d2. Đường chéo đầu tiên (d1) nối hai đỉnh đối diện, trong khi đường chéo thứ hai (d2) nối hai đỉnh còn lại. Bên cạnh đó, diện tích của hình thoi có thể được tính bằng công thức:
\[ S = \frac{d1 \times d2}{2} \]
Trong đó, S là diện tích của hình thoi. Nhờ vào công thức này, nếu biết được diện tích và độ dài một trong hai đường chéo, ta có thể dễ dàng tính được độ dài đường chéo còn lại.

Cách tính đường chéo khi biết diện tích
Nếu bạn đã biết diện tích S của hình thoi và độ dài của một trong hai đường chéo, bạn có thể dễ dàng tính được độ dài của đường chéo còn lại bằng cách sử dụng công thức:
\[ d2 = \frac{2S}{d1} \]
Trong đó, d1 là độ dài của đường chéo đã biết. Ví dụ, nếu diện tích của hình thoi là 100 cm² và độ dài của đường chéo d1 là 20 cm, thì:
\[ d2 = \frac{2 \times 100}{20} = 10 \text{ cm} \]
Ngược lại, nếu bạn muốn tìm đường chéo d1 khi biết d2 và S, bạn có thể áp dụng công thức sau:
\[ d1 = \frac{2S}{d2} \]
Điều này cho phép tính toán một cách linh hoạt dựa trên thông tin có sẵn.
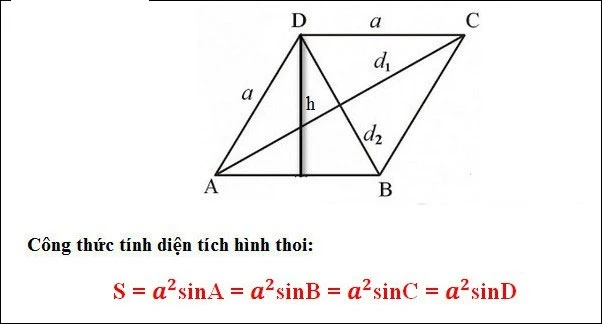
Tính đường chéo từ cạnh của hình thoi
Ngoài việc tính toán đường chéo từ diện tích, bạn cũng có thể tính độ dài của đường chéo từ độ dài cạnh của hình thoi. Nếu bạn biết độ dài của cạnh a, bạn có thể sử dụng công thức sau để tính độ dài của hai đường chéo:
\[ d1 = a \sqrt{2 + 2 \cos(\alpha)} \]
\[ d2 = a \sqrt{2 - 2 \cos(\alpha)} \]
Trong đó, α là góc giữa hai cạnh liền kề của hình thoi. Nếu bạn không biết góc α, nhưng biết rằng hình thoi là hình vuông (tức là α = 90 độ), thì đường chéo có thể được tính bằng công thức đơn giản:
\[ d = a \sqrt{2} \]
Hình vuông là một trường hợp đặc biệt của hình thoi, nơi các góc bằng 90 độ.
Ví dụ thực tế và bài tập
Để hiểu rõ hơn về cách tính toán, chúng ta hãy cùng làm một số bài tập thực tế.
Bài tập 1
Cho hình thoi có diện tích 50 cm² và một trong hai đường chéo có độ dài là 10 cm. Tính đường chéo còn lại.
Giải:
Sử dụng công thức:
\[ d2 = \frac{2S}{d1} = \frac{2 \times 50}{10} = 10 \text{ cm} \]
Bài tập 2
Cho hình thoi có cạnh dài 6 cm và góc giữa hai cạnh là 60 độ. Tính độ dài của hai đường chéo.
Giải:
Đầu tiên, tính độ dài đường chéo d1 và d2 bằng công thức đã đề cập ở trên.
\[ d1 = 6 \sqrt{2 + 2 \cos(60)} = 6 \sqrt{2 + 1} = 6 \sqrt{3} \approx 10.39 \text{ cm} \]
\[ d2 = 6 \sqrt{2 - 2 \cos(60)} = 6 \sqrt{2 - 1} = 6 \times 1 = 6 \text{ cm} \]
Kết luận, độ dài hai đường chéo của hình thoi là khoảng 10.39 cm và 6 cm.
Kết luận
Như vậy, việc tính toán độ dài của đường chéo hình thoi không chỉ đơn giản mà còn rất hữu ích, đặc biệt trong việc áp dụng các kiến thức hình học vào thực tế. Với các công thức đã được trình bày, bạn có thể dễ dàng tính toán được độ dài các đường chéo dựa trên diện tích hoặc cạnh của hình thoi. Hy vọng rằng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn nắm rõ hơn về hình thoi trong hình học.
Đừng quên thực hành nhiều bài tập để củng cố kiến thức và kỹ năng của mình nhé!