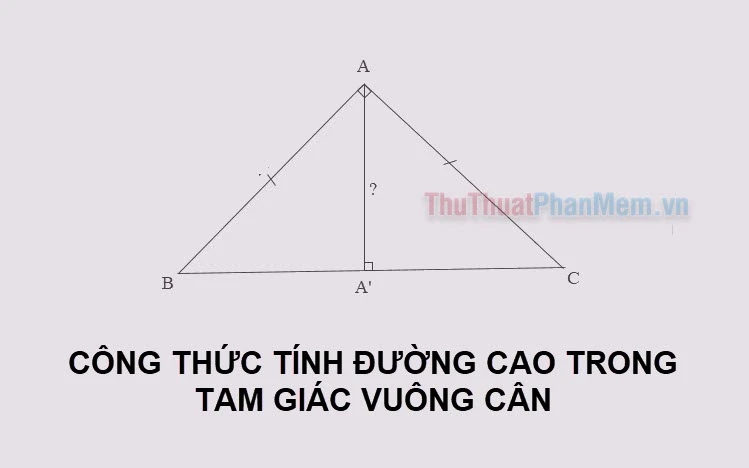
Giới thiệu về Đường cao trong Tam giác Vuông Cân
Tam giác vuông cân là một trong những hình dạng cơ bản trong hình học, được biết đến với hai cạnh góc vuông bằng nhau và một cạnh huyền. Một trong những yếu tố quan trọng trong tam giác vuông cân là đường cao, được xác định từ đỉnh góc vuông đến cạnh huyền. Đường cao không chỉ giúp chúng ta tính diện tích hay thể hiện các tính chất hình học mà còn là một phần không thể thiếu trong các bài toán liên quan đến tam giác. Trong bài viết này, chúng ta sẽ cùng nhau khám phá phương pháp tính đường cao trong tam giác vuông cân, từ định nghĩa, công thức đến ví dụ minh họa.
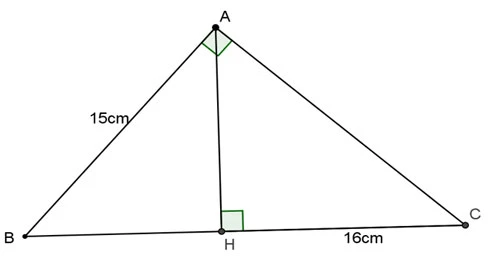
Tính chất của Đường cao trong Tam giác Vuông Cân
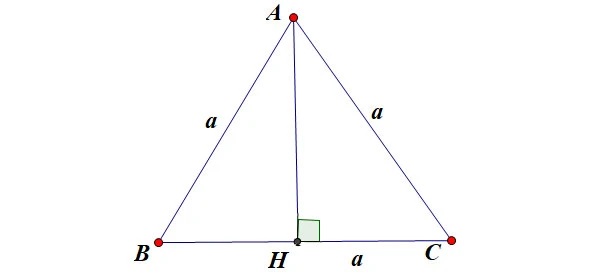
Đường cao trong tam giác vuông cân có nhiều tính chất thú vị. Đầu tiên, đường cao kẻ từ đỉnh góc vuông sẽ chia tam giác thành hai tam giác vuông nhỏ hơn, và cả hai tam giác này đều có tính chất tương tự như tam giác ban đầu. Điều này có nghĩa là nếu bạn biết độ dài cạnh huyền, bạn có thể dễ dàng tính độ dài của các cạnh còn lại.
Ngoài ra, trong tam giác vuông cân, đường cao cũng đồng thời là đường trung tuyến và đường phân giác. Điều này có nghĩa là nó chia cạnh huyền thành hai phần bằng nhau. Tính chất này rất quan trọng trong việc giải các bài toán hình học và giúp đơn giản hóa nhiều công thức.
Công thức Tính đường cao trong Tam giác Vuông Cân
Để tính chiều dài của đường cao trong tam giác vuông cân, có một số công thức cơ bản mà bạn có thể áp dụng. Một trong những công thức phổ biến nhất là:
\[ h = \frac{a \cdot b}{c} \]
Trong đó:
- \( h \) là độ dài của đường cao,
- \( a \) và \( b \) là độ dài của hai cạnh góc vuông,
- \( c \) là độ dài của cạnh huyền.
Ngoài ra, bạn cũng có thể tính đường cao bằng cách sử dụng định lý Pythagore, nếu đã biết độ dài các cạnh của tam giác:
\[ h^2 = b' \cdot c' \]
Trong đó \( b' \) và \( c' \) là các đoạn thẳng mà đường cao chia cạnh huyền ra. Công thức này giúp bạn tính được chiều cao một cách chính xác mà không cần phải biết đến các độ dài cụ thể của các cạnh.
Ví dụ Minh họa
Để giúp bạn hiểu rõ hơn về cách tính đường cao trong tam giác vuông cân, hãy cùng xem qua một ví dụ cụ thể.
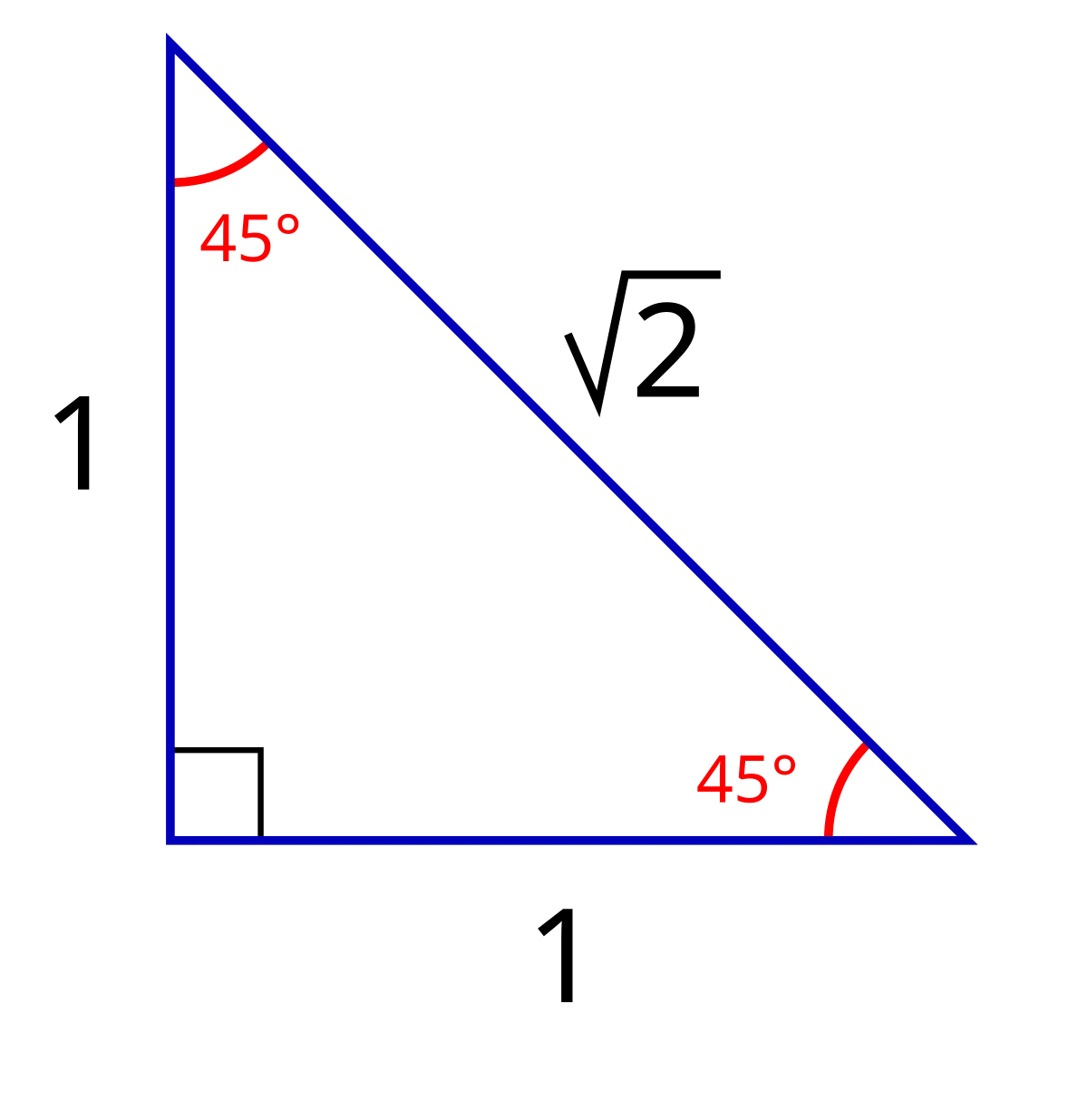
Giả sử chúng ta có một tam giác vuông cân với hai cạnh góc vuông dài 4 cm. Để tính chiều dài đường cao \( h \), trước tiên chúng ta cần tính cạnh huyền \( c \) bằng định lý Pythagore:
\[ c = \sqrt{a^2 + b^2} = \sqrt{4^2 + 4^2} = \sqrt{32} = 4\sqrt{2} \]
Bây giờ, chúng ta áp dụng công thức để tính đường cao:
\[ h = \frac{a \cdot b}{c} = \frac{4 \cdot 4}{4\sqrt{2}} = \frac{16}{4\sqrt{2}} = \frac{4\sqrt{2}}{2} = 2\sqrt{2} \]
Vậy chiều dài đường cao trong tam giác vuông cân này là \( 2\sqrt{2} \) cm.
Kết luận
Việc tính đường cao trong tam giác vuông cân không chỉ giúp bạn giải quyết các bài toán hình học mà còn là một kỹ năng quan trọng trong nhiều lĩnh vực khác nhau. Với các công thức đơn giản và tính chất tuyệt vời của nó, đường cao trong tam giác vuông cân thực sự là một khía cạnh thú vị của hình học.
Để ôn lại, hãy nhớ rằng: Đường cao trong tam giác vuông cân không chỉ là một đoạn thẳng mà còn là cầu nối giữa các tính chất hình học, giúp ta hiểu rõ hơn về cấu trúc và mối quan hệ giữa các cạnh trong tam giác. Hãy thử áp dụng những công thức này vào các bài toán khác nhau để tăng cường khả năng tư duy và giải quyết vấn đề của bạn.
Hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích và thú vị về cách tính đường cao trong tam giác vuông cân. Nếu bạn có bất kỳ câu hỏi nào hoặc cần thêm thông tin, đừng ngần ngại để lại câu hỏi trong phần bình luận bên dưới!
