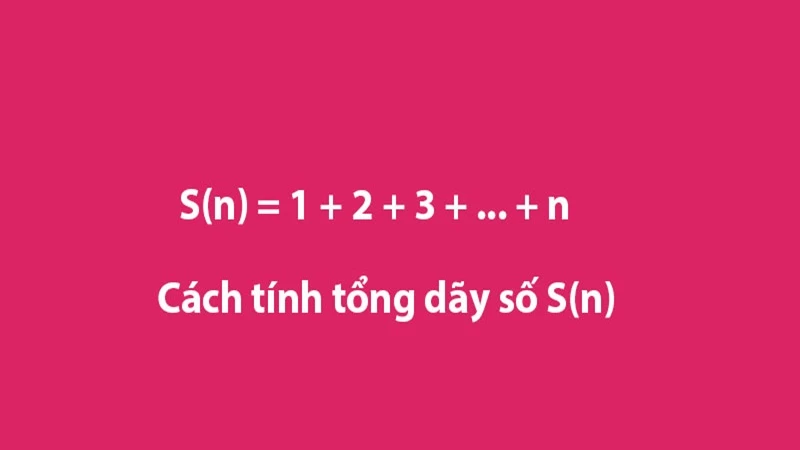Giới thiệu về dãy số và tầm quan trọng của việc tính tổng
Dãy số là một trong những khái niệm cơ bản trong toán học mà tất cả chúng ta đều đã từng tiếp xúc từ khi còn học tiểu học. Một dãy số có thể được định nghĩa là một tập hợp các số, được sắp xếp theo một quy luật nhất định. Trong đó, dãy số cách đều là một dạng đặc biệt của dãy số, trong đó khoảng cách giữa các số hạng là không thay đổi. Việc tính tổng của các số hạng trong dãy số cách đều không chỉ giúp ích cho việc giải bài toán trong sách giáo khoa mà còn có thể áp dụng trong nhiều lĩnh vực khác nhau như thống kê, tài chính, và khoa học máy tính.
Cấu trúc của dãy số cách đều
Dãy số cách đều có thể được biểu diễn theo công thức sau:
- \( a_n = a_1 + (n - 1) \cdot d \)
Trong đó:
- \( a_n \) là số hạng thứ n trong dãy số.
- \( a_1 \) là số hạng đầu tiên.
- \( d \) là khoảng cách giữa các số hạng.
- \( n \) là chỉ số của số hạng cần tìm.
Ví dụ, nếu dãy số bắt đầu từ 3 và tăng thêm 2 mỗi bước, ta có dãy số: 3, 5, 7, 9, 11, ...
Ở đây, số hạng đầu tiên \( a_1 = 3 \) và khoảng cách \( d = 2 \).
Cách tính tổng của dãy số cách đều
Để tính tổng của dãy số cách đều, ta có công thức tổng quát như sau:
- \( S_n = \frac{n}{2} \cdot (a_1 + a_n) \)
Trong đó:
- \( S_n \) là tổng của n số hạng.
- \( n \) là số lượng số hạng trong dãy.
- \( a_1 \) là số hạng đầu tiên.
- \( a_n \) là số hạng cuối cùng trong dãy.
Ngoài ra, nếu ta biết khoảng cách \( d \), ta cũng có thể tính được tổng dãy số cách đều bằng công thức sau:
- \( S_n = \frac{n}{2} \cdot (2a_1 + (n - 1) \cdot d) \)
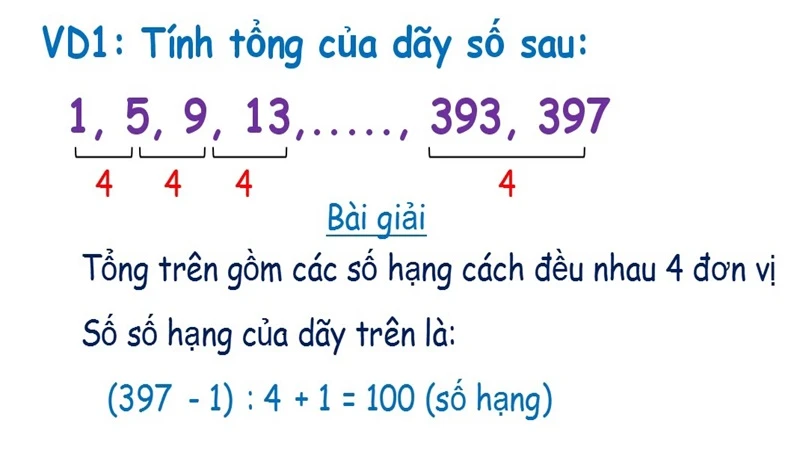
Ví dụ minh họa
Giả sử ta cần tính tổng của dãy số cách đều bắt đầu từ 1, với 10 số hạng và khoảng cách giữa các số hạng là 2. Ta có:
- Số hạng đầu tiên \( a_1 = 1 \)
- Số hạng thứ 10 \( a_{10} = 1 + (10 - 1) \cdot 2 = 19 \)
- Số lượng số hạng \( n = 10 \)
Áp dụng vào công thức tính tổng:
\[
S_{10} = \frac{10}{2} \cdot (1 + 19) = 5 \cdot 20 = 100
\]
Như vậy, tổng của dãy số cách đều này là 100.

Ứng dụng của việc tính tổng dãy số cách đều
Việc tính tổng của dãy số cách đều có nhiều ứng dụng trong cuộc sống và các lĩnh vực khác nhau. Dưới đây là một số ứng dụng cụ thể:
1. Trong thống kê
Trong thống kê, chúng ta thường sử dụng dãy số để biểu diễn các dữ liệu thu thập được. Việc tính tổng giúp chúng ta nhanh chóng nắm bắt được tổng giá trị của một tập hợp dữ liệu.
2. Trong tài chính
Trong lĩnh vực tài chính, việc tính tổng các khoản chi tiêu hoặc thu nhập hàng tháng cũng có thể được xem như là một bài toán về dãy số cách đều. Ví dụ, nếu một người nhận được một số tiền cố định mỗi tháng, việc tính tổng trong một khoảng thời gian nhất định sẽ giúp họ biết được tổng số tiền mình đã nhận.
3. Trong khoa học máy tính
Trong lập trình, thuật toán tính tổng dãy số cách đều có thể được áp dụng để tối ưu hóa hiệu suất khi xử lý các tập dữ liệu lớn. Việc tính toán nhanh chóng và hiệu quả giúp tiết kiệm thời gian và tài nguyên.
Một số bài tập thực hành
Để nắm vững kiến thức về cách tính tổng của dãy số cách đều, bạn có thể tham khảo một số bài tập thực hành dưới đây:
Bài tập 1
Tính tổng của dãy số cách đều bắt đầu từ 5, với 10 số hạng và khoảng cách giữa các số hạng là 3.
Bài tập 2
Cho dãy số 2, 4, 6, ..., 50. Hãy tính tổng của dãy số này.
Bài tập 3
Nếu một dãy số cách đều có 20 số hạng, số hạng đầu tiên là 10 và khoảng cách là 5, hãy tính tổng của dãy số này.
Kết luận
Tính tổng của dãy số cách đều là một trong những kỹ năng cơ bản nhưng vô cùng quan trọng trong toán học. Nó không chỉ giúp chúng ta giải quyết các bài toán học thuật mà còn ứng dụng trong nhiều lĩnh vực thực tiễn khác nhau. Hiểu rõ về công thức và cách tính tổng sẽ giúp bạn trở thành một người làm toán giỏi và tự tin hơn trong việc giải quyết các vấn đề liên quan đến dãy số.
Hãy luyện tập thường xuyên để nắm vững kiến thức này và áp dụng vào cuộc sống hàng ngày của bạn!