Chu vi của một hình tròn là một khái niệm cơ bản trong toán học, có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau từ kiến trúc, thiết kế đến kỹ thuật. Hiểu rõ cách tính chu vi sẽ giúp bạn dễ dàng hơn trong việc giải quyết các bài toán liên quan đến hình tròn. Trong bài viết này, chúng ta sẽ cùng khám phá các khía cạnh liên quan đến chu vi của hình tròn, bao gồm định nghĩa, công thức tính toán, mối liên hệ với các yếu tố khác và một số ví dụ minh họa.
Định nghĩa chu vi hình tròn
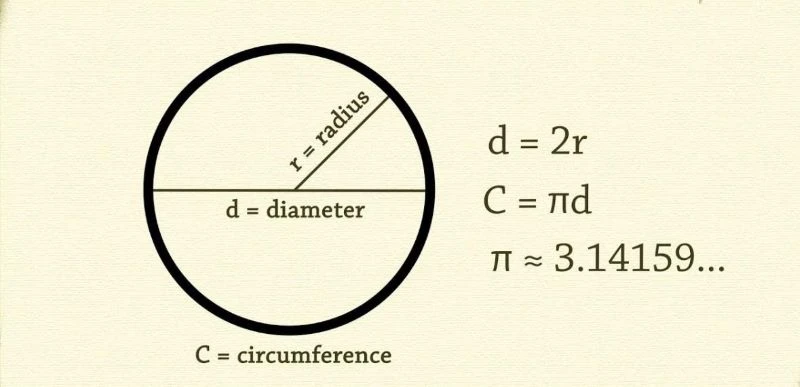
Chu vi hình tròn là độ dài của đường biên giới của hình tròn. Đường biên này được xác định bởi một điểm cố định, gọi là tâm, và tất cả các điểm nằm trên một khoảng cách cố định, gọi là bán kính. Chu vi thường được ký hiệu bằng chữ cái C. Hình tròn có nhiều ứng dụng trong thực tế, từ thiết kế các sản phẩm tròn đến việc tính toán diện tích mặt bằng.
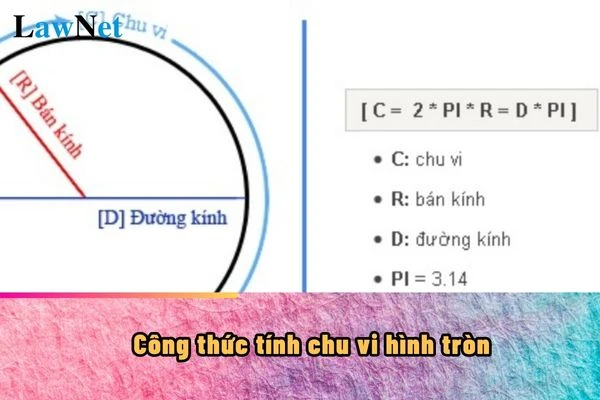
Công thức tính chu vi
Để tính chu vi của hình tròn, chúng ta có thể sử dụng hai công thức chính:
- Dựa vào đường kính: Chu vi được tính bằng công thức:
C = d × π
Trong đó:
- C là chu vi,
- d là đường kính của hình tròn,
- π (pi) xấp xỉ bằng 3,14.
- Dựa vào bán kính: Nếu bạn biết bán kính (r) của hình tròn, công thức sẽ là:
C = 2 × r × π
Trong đó:
- r là bán kính, tức là khoảng cách từ tâm đến bất kỳ điểm nào trên đường tròn.
Cả hai công thức trên đều cho kết quả giống nhau, vì bán kính và đường kính có mối liên hệ là d = 2 × r. Điều này có nghĩa là bạn có thể linh hoạt trong việc sử dụng công thức nào tùy thuộc vào thông tin đã biết.
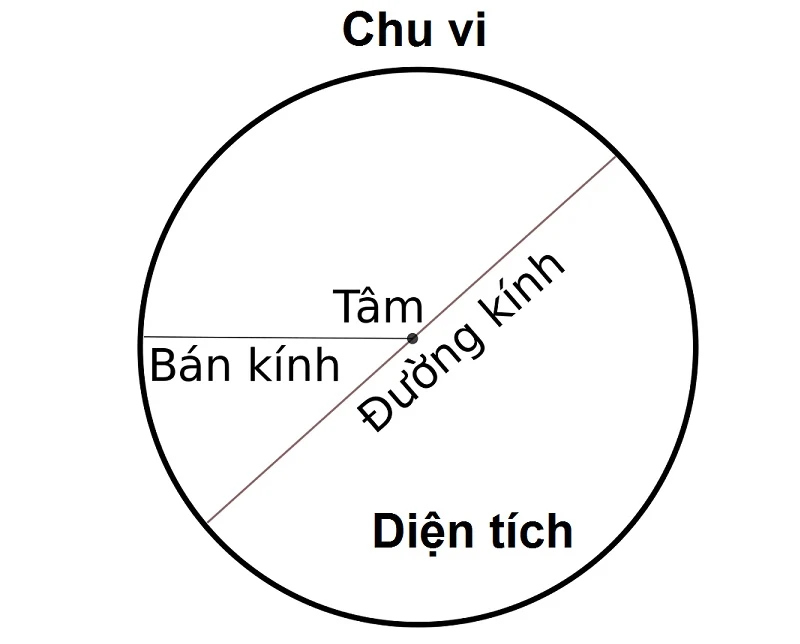
Mối liên hệ giữa các yếu tố trong hình tròn
Một hình tròn được xác định bởi ba yếu tố chính: tâm, bán kính và đường kính. Trong đó, bán kính là khoảng cách từ tâm đến bất kỳ điểm nào trên đường tròn, trong khi đường kính là khoảng cách từ một điểm trên đường tròn này đến một điểm đối diện qua tâm. Dưới đây là một số mối liên hệ quan trọng giữa các yếu tố này:
- Đường kính: Đường kính là gấp đôi bán kính, tức là d = 2 × r.
- Số pi (π): Số π là một hằng số toán học mà giá trị gần đúng nhất là 3,14. Số này xuất hiện trong nhiều công thức liên quan đến hình tròn, không chỉ chu vi mà còn cả diện tích.
- Chu vi và diện tích: Ngoài chu vi, hình tròn còn có diện tích, được tính bằng công thức S = π × r². Khi biết chu vi, bạn cũng có thể dễ dàng tính diện tích nếu biết cách chuyển đổi giữa chu vi và bán kính.
Ví dụ minh họa thực tế
Để giúp bạn hiểu rõ hơn về cách tính chu vi hình tròn, chúng ta hãy cùng xem xét một số ví dụ cụ thể.
Ví dụ 1: Tính chu vi hình tròn khi biết bán kính
Giả sử bạn có một hình tròn có bán kính là 5 cm. Để tính chu vi, bạn sử dụng công thức:
C = 2 × r × π
C = 2 × 5 × 3,14 = 31,4 cm.
Vậy chu vi của hình tròn này là 31,4 cm.
Ví dụ 2: Tính chu vi hình tròn khi biết đường kính
Nếu đường kính của hình tròn là 10 cm, bạn sẽ làm như sau:
C = d × π
C = 10 × 3,14 = 31,4 cm.
Chu vi của hình tròn này cũng là 31,4 cm, cho thấy sự nhất quán trong các phương pháp tính toán.
Những ứng dụng trong thực tế
Chu vi hình tròn có nhiều ứng dụng thiết thực trong cuộc sống hàng ngày. Một số ví dụ điển hình bao gồm:
- Thiết kế công trình: Khi thiết kế các công trình có hình dáng tròn như cột, bể, hay sân thể thao, việc tính toán chính xác chu vi là rất quan trọng để đảm bảo tính thẩm mỹ và công năng sử dụng.
- Sản xuất đồ vật: Nhiều sản phẩm như bánh xe, đồng hồ, hay các đồ vật hình tròn khác yêu cầu việc tính chu vi để tối ưu hóa kích thước và vật liệu sử dụng.
- Giải quyết bài toán thực tế: Trong nhiều bài toán thực tế, bạn sẽ cần phải tính chu vi để tìm ra diện tích, chi phí vật liệu, hoặc thời gian di chuyển xung quanh hình tròn.
Như vậy, việc nắm rõ cách tính chu vi hình tròn không chỉ giúp bạn trong học tập mà còn có thể áp dụng vào nhiều lĩnh vực khác trong cuộc sống.
Kết luận
Chu vi của hình tròn là một khái niệm quan trọng trong toán học và có nhiều ứng dụng thiết thực trong cuộc sống hàng ngày. Bằng cách hiểu rõ các công thức và mối liên hệ giữa các yếu tố trong hình tròn, bạn có thể dễ dàng tính toán chu vi cho bất kỳ hình tròn nào. Hy vọng rằng bài viết này sẽ cung cấp cho bạn những kiến thức bổ ích và giúp bạn tự tin hơn trong việc giải quyết các bài toán liên quan đến hình tròn.
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách tính chu vi hình tròn và những ứng dụng của nó. Hãy thực hành nhiều hơn để củng cố kiến thức của mình nhé!
