Hướng Dẫn Tính Diện Tích Của Một Hình Tam Giác
Hình tam giác là một trong những hình dạng cơ bản nhất trong hình học. Chúng xuất hiện trong nhiều lĩnh vực, từ xây dựng cho đến nghệ thuật. Việc nắm vững cách tính diện tích của hình tam giác sẽ giúp bạn trong việc giải quyết nhiều bài toán thực tiễn. Trong bài viết này, chúng ta sẽ cùng tìm hiểu cách tính diện tích của một hình tam giác thường, bao gồm các công thức, ví dụ minh họa và ứng dụng thực tế.
1. Công Thức Tính Diện Tích Hình Tam Giác
Diện tích của hình tam giác thường được tính bằng công thức:
\[ S = \frac{1}{2} \times b \times h \]
Trong đó:
- \( S \) là diện tích của tam giác.
- \( b \) là độ dài của cạnh đáy.
- \( h \) là chiều cao hạ từ đỉnh của tam giác xuống cạnh đáy.
Công thức này rất đơn giản và có thể áp dụng cho mọi loại tam giác, miễn là bạn biết chiều cao và cạnh đáy của nó. Để dễ hình dung, hãy xem hình ảnh sau:
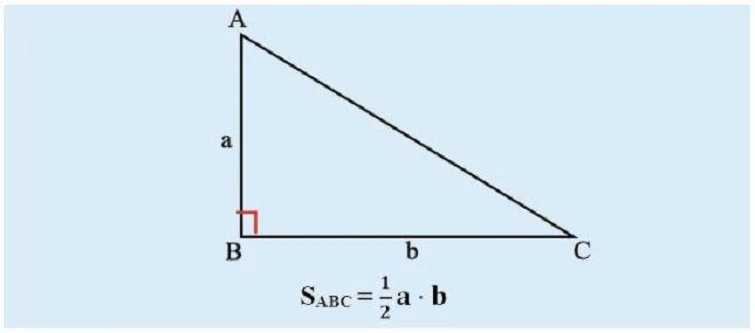
2. Cách Tìm Chiều Cao Của Tam Giác
Chiều cao của tam giác là đoạn thẳng vẽ từ một đỉnh của tam giác vuông góc với cạnh đối diện. Để tìm chiều cao này, bạn cần thực hiện các bước sau:
- Bước 1: Xác định cạnh đáy mà bạn muốn tính chiều cao.
- Bước 2: Thực hiện vẽ một đường thẳng từ đỉnh của tam giác xuống cạnh đáy sao cho đường thẳng này vuông góc với cạnh đáy.
- Bước 3: Đo độ dài của đoạn thẳng này, chính là chiều cao bạn cần tìm.
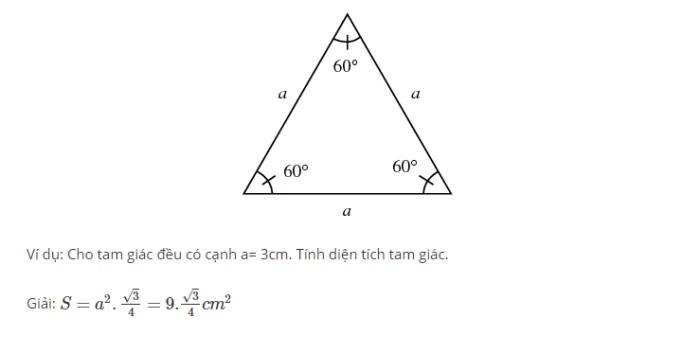
Nếu bạn có một tam giác đều, chiều cao có thể được tính bằng công thức:
\[ h = \frac{\sqrt{3}}{2} a \]
Trong đó \( a \) là độ dài cạnh của tam giác đều.
3. Ví Dụ Minh Họa Về Tính Diện Tích Tam Giác
Để giúp bạn hiểu rõ hơn về cách tính diện tích của tam giác, dưới đây là một ví dụ cụ thể:
Ví dụ 1: Cho một tam giác có cạnh đáy dài 10 cm và chiều cao hạ từ đỉnh xuống cạnh đáy là 6 cm. Tính diện tích của tam giác này.
Áp dụng công thức, ta có:
\[ S = \frac{1}{2} \times 10 \times 6 = 30 \text{ cm}^2 \]
Ví dụ 2: Tính diện tích của một tam giác đều có cạnh dài 8 cm.
Đầu tiên, ta tính chiều cao của tam giác đều:
\[ h = \frac{\sqrt{3}}{2} \times 8 = 4\sqrt{3} \text{ cm} \]
Sau đó, áp dụng công thức tính diện tích:
\[ S = \frac{1}{2} \times 8 \times 4\sqrt{3} = 16\sqrt{3} \text{ cm}^2 \]
Kết quả là diện tích của tam giác đều này là khoảng 27.7 cm².
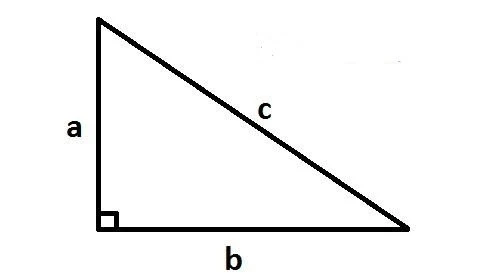
4. Ứng Dụng Thực Tế Của Tính Diện Tích Tam Giác
Diện tích của hình tam giác không chỉ có ý nghĩa trong toán học mà còn có nhiều ứng dụng thực tế. Dưới đây là một số ví dụ về ứng dụng của việc tính diện tích tam giác:
- Xây Dựng: Trong ngành xây dựng, việc tính diện tích của các mặt phẳng hình tam giác giúp xác định lượng vật liệu cần thiết, giúp tiết kiệm chi phí và thời gian thi công.
- Thiết Kế Nghệ Thuật: Nhiều tác phẩm nghệ thuật sử dụng hình tam giác trong thiết kế, vì vậy việc hiểu rõ về diện tích của nó sẽ giúp nghệ sĩ có thể bố trí các yếu tố một cách hợp lý.
- Khoa Học Tự Nhiên: Trong các nghiên cứu về địa lý hoặc sinh thái, việc tính diện tích của các khu vực hình tam giác giúp các nhà khoa học đánh giá được các yếu tố như diện tích rừng, hồ, hay đất nông nghiệp.
Việc nắm vững cách tính diện tích hình tam giác sẽ không chỉ giúp bạn trong học tập mà còn giúp bạn trong nhiều lĩnh vực khác nhau trong cuộc sống. Hãy tiếp tục thực hành và áp dụng công thức này trong mọi tình huống phù hợp.
Kết Luận
Việc tính diện tích của hình tam giác là một kỹ năng cơ bản nhưng rất hữu ích. Với công thức đơn giản và những bước thực hiện rõ ràng, bạn hoàn toàn có thể áp dụng để giải quyết nhiều vấn đề khác nhau trong thực tế. Hãy nhớ rằng, ngoài việc biết công thức, việc thực hành và áp dụng chúng vào các bài toán thực tế sẽ giúp bạn ghi nhớ lâu hơn và phát triển kỹ năng toán học của mình.
Hy vọng rằng qua bài viết này, bạn đã có cái nhìn sâu sắc hơn về cách tính diện tích của hình tam giác và những ứng dụng thực tiễn của nó. Hãy thực hiện các bài tập và nâng cao khả năng của bản thân trong lĩnh vực này nhé!