Giới thiệu về hình tam giác cân
Hình tam giác là một trong những hình học cơ bản và thường gặp trong toán học. Trong số các loại tam giác, hình tam giác cân được biết đến với sự đối xứng đặc biệt của nó. Hình tam giác cân có hai cạnh bằng nhau và hai góc đối diện với chúng cũng bằng nhau. Đặc điểm này không chỉ tạo nên vẻ đẹp hài hòa mà còn giúp chúng ta dễ dàng tính toán các yếu tố liên quan đến hình tam giác này, trong đó có diện tích.
Định nghĩa và tính chất của tam giác cân
Hình tam giác cân có các đặc điểm nổi bật như:
- Hai cạnh bằng nhau: Gọi là cạnh bên, có độ dài a.
- Cạnh đáy: Gọi là b, là cạnh không bằng với hai cạnh bên.
- Chiều cao: Là đoạn thẳng vuông góc từ đỉnh đối diện với cạnh đáy xuống cạnh đáy, được ký hiệu là h.
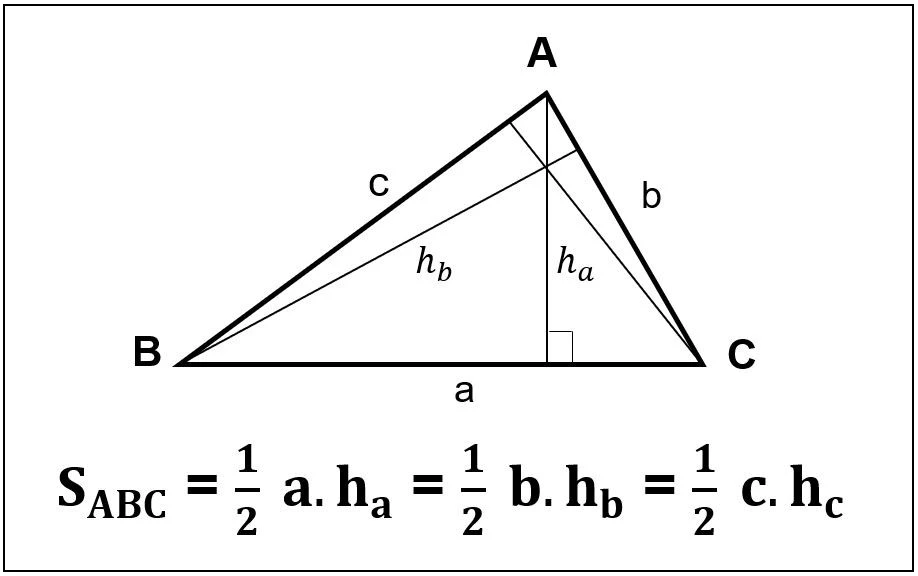
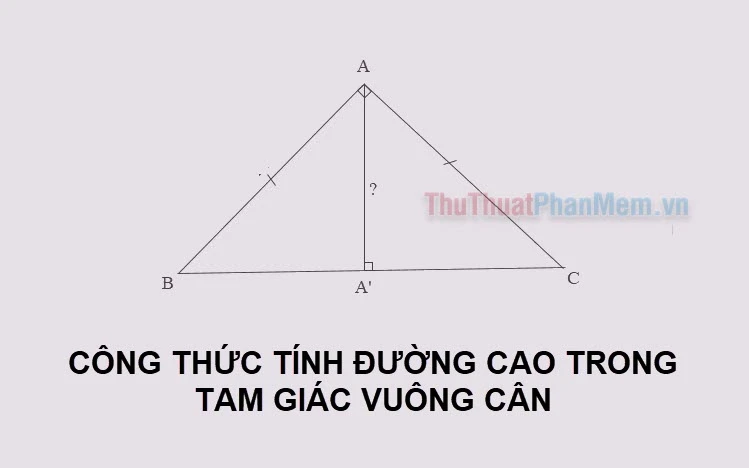
Để dễ hình dung, dưới đây là hình ảnh minh họa cho một hình tam giác cân:
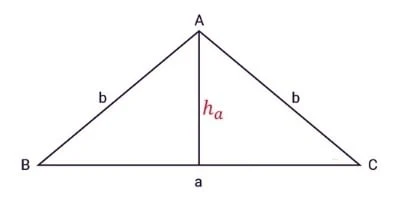
Như đã đề cập, hai cạnh bên của tam giác cân bằng nhau, trong khi cạnh đáy có thể có độ dài khác. Với các tính chất này, việc tính diện tích của một hình tam giác cân trở nên đơn giản hơn.
Công thức tính diện tích hình tam giác cân
Khi tính diện tích của một hình tam giác cân, chúng ta sử dụng công thức sau:
\[ S = \frac{1}{2} \times b \times h \]
Trong đó:
- \( S \) là diện tích của tam giác.
- \( b \) là độ dài cạnh đáy.
- \( h \) là chiều cao từ đỉnh xuống cạnh đáy.
Công thức này cho phép chúng ta tính diện tích một cách nhanh chóng và dễ dàng khi đã biết chiều cao và cạnh đáy. Cùng xem xét một ví dụ minh họa:
Giả sử cạnh đáy \( b = 10 \) cm và chiều cao \( h = 8 \) cm, ta có:
\[ S = \frac{1}{2} \times 10 \times 8 = 40 \text{ cm}^2 \]
Hình ảnh minh họa công thức
Dưới đây là hình ảnh minh họa công thức tính diện tích tam giác:
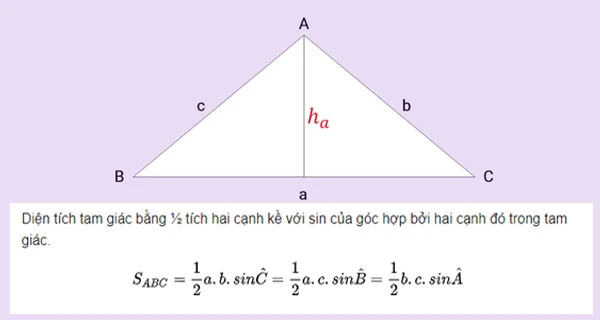
Các phương pháp tính chiều cao trong tam giác cân
Để tính diện tích của tam giác cân, trước tiên chúng ta cần biết chiều cao. Có một số phương pháp để tính chiều cao này, tùy thuộc vào thông tin đã cho:
1. Biết độ dài cạnh đáy và cạnh bên
Nếu chúng ta biết độ dài của cạnh đáy \( b \) và cạnh bên \( a \), chúng ta có thể tính chiều cao \( h \) bằng cách sử dụng định lý Pythagore. Với tam giác cân, chiều cao sẽ chia tam giác thành hai tam giác vuông.
Công thức tính chiều cao sẽ là:
\[ h = \sqrt{a^2 - \left(\frac{b}{2}\right)^2} \]
2. Biết góc ở đỉnh
Nếu bạn biết độ dài một cạnh đáy \( b \) và góc ở đỉnh \( A \) (góc giữa hai cạnh bên), bạn có thể tính chiều cao bằng cách sử dụng sin:
\[ h = \frac{b}{2} \times \tan\left(\frac{A}{2}\right) \]
3. Sử dụng công thức chiều cao từ diện tích
Khi đã tính được diện tích \( S \), bạn có thể tính chiều cao bằng cách đảo ngược công thức diện tích:
\[ h = \frac{2S}{b} \]
Các phương pháp này sẽ giúp bạn dễ dàng tính được chiều cao cần thiết để tính diện tích tam giác cân.
Một số ví dụ cụ thể
Để củng cố kiến thức, hãy cùng nhau xem xét một số ví dụ tính diện tích của hình tam giác cân.
Ví dụ 1: Tính diện tích tam giác cân khi biết cạnh đáy và chiều cao
Giả sử có một tam giác cân với cạnh đáy \( b = 12 \) cm và chiều cao \( h = 5 \) cm.
Áp dụng công thức:
\[ S = \frac{1}{2} \times 12 \times 5 = 30 \text{ cm}^2 \]
Ví dụ 2: Tính diện tích tam giác cân khi biết cạnh đáy và cạnh bên
Giả sử điểm \( B \) và điểm \( C \) là hai đỉnh của cạnh đáy \( b = 14 \) cm. Độ dài cạnh bên \( a = 10 \) cm. Để tính chiều cao \( h \), chúng ta sử dụng định lý Pythagore:
\[ h = \sqrt{10^2 - \left(\frac{14}{2}\right)^2} = \sqrt{100 - 49} = \sqrt{51} \approx 7.14 \text{ cm} \]
Sau đó, sử dụng công thức tính diện tích:
\[ S = \frac{1}{2} \times 14 \times 7.14 \approx 49.98 \text{ cm}^2 \]
Ví dụ 3: Sử dụng góc trong tam giác
Giả sử bạn có tam giác cân với cạnh đáy \( b = 9 \) cm và góc ở đỉnh \( A = 60^\circ \).
Sử dụng công thức tính chiều cao:
\[ h = \frac{9}{2} \times \tan\left(\frac{60}{2}\right) = \frac{9}{2} \times \tan(30^\circ) \approx \frac{9}{2} \times 0.577 = 2.59 \text{ cm} \]
Sau đó, tính diện tích:
\[ S = \frac{1}{2} \times 9 \times 2.59 \approx 11.66 \text{ cm}^2 \]
Kết luận
Tính diện tích của hình tam giác cân tưởng chừng đơn giản nhưng lại rất thú vị. Qua bài viết này, bạn đã nắm được những kiến thức cơ bản về tam giác cân, công thức tính diện tích, cũng như các phương pháp tìm chiều cao. Bằng cách áp dụng các công thức và ví dụ minh họa ở trên, bạn có thể tự tin giải quyết các bài toán liên quan đến diện tích của tam giác cân.
Nếu bạn cần thêm thông tin hoặc có thắc mắc nào khác về hình học, đừng ngần ngại tham khảo thêm tài liệu hoặc hỏi các chuyên gia trong lĩnh vực. Hãy tiếp tục khám phá và học hỏi thêm về các hình học khác để làm phong phú thêm kiến thức của mình.
