Bán kính hình tròn và các công thức tính toán cần thiết

Hình tròn là một trong những hình học cơ bản và quen thuộc nhất trong toán học. Nó xuất hiện trong nhiều lĩnh vực khác nhau từ địa lý, vật lý cho đến nghệ thuật. Để tìm hiểu về hình tròn, một trong những khái niệm quan trọng mà bạn cần nắm rõ đó là bán kính. Trong bài viết này, chúng ta sẽ đi sâu vào cách xác định bán kính hình tròn thông qua nhiều phương pháp khác nhau, cùng với một số ứng dụng hữu ích trong thực tế.

Định nghĩa và ý nghĩa của bán kính

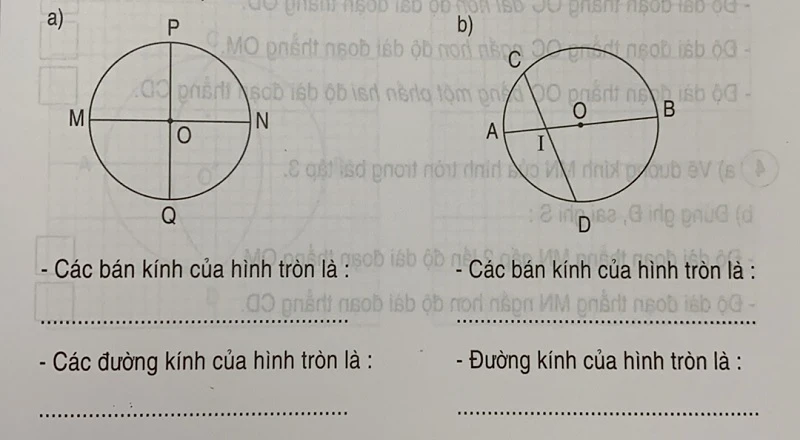
Bán kính là khoảng cách từ tâm của hình tròn đến bất kỳ điểm nào trên đường tròn. Cụ thể, nếu bạn vẽ một đường tròn với tâm là điểm O và một điểm A nằm trên đường tròn, thì đoạn thẳng OA chính là bán kính của hình tròn đó.

Tìm hiểu về các yếu tố liên quan

Để hiểu rõ hơn về bán kính, chúng ta cũng cần biết đến một số khái niệm liên quan:

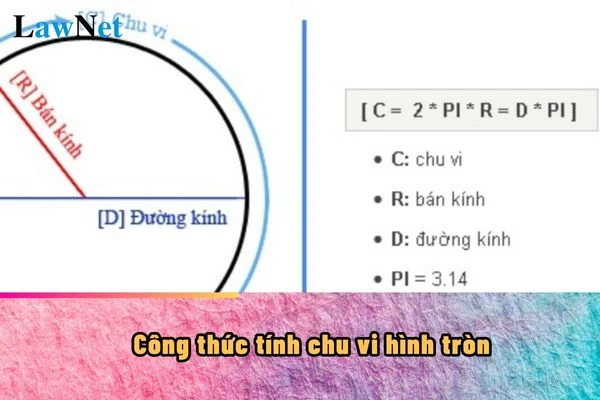
• Đường kính: Là đoạn thẳng nối hai điểm trên đường tròn đi qua tâm. Đường kính luôn gấp đôi bán kính. Công thức tính đường kính là:

\[ d = 2r \] trong đó \( d \) là đường kính, \( r \) là bán kính.

• Chu vi: Là chiều dài của đường viền xung quanh hình tròn. Công thức tính chu vi hình tròn là:

\[ C = 2\pi r \] với \( \pi \) khoảng 3.14.

• Diện tích: Là không gian bên trong hình tròn. Công thức tính diện tích là:

\[ S = \pi r^2 \]

Cách tính bán kính từ chu vi

Một trong những phương pháp phổ biến để tính bán kính là dựa vào chu vi của hình tròn. Nếu bạn biết chu vi, bạn có thể áp dụng công thức sau để tìm bán kính:

Công thức

\[ r = \frac{C}{2\pi} \]

Ví dụ minh họa

Giả sử chu vi của một hình tròn là 31.4 cm. Để tìm bán kính, bạn sẽ làm như sau:

• Thay giá trị chu vi vào công thức:

\[ r = \frac{31.4}{2\pi} \approx \frac{31.4}{6.28} \approx 5 \] Vậy bán kính của hình tròn là 5 cm.

Cách tính bán kính từ đường kính

Nếu bạn biết đường kính của hình tròn, việc tính bán kính trở nên đơn giản hơn rất nhiều. Như đã đề cập ở phần trước, bán kính là một nửa của đường kính. Công thức để tính bán kính lúc này sẽ là:

Công thức

\[ r = \frac{d}{2} \]

Ví dụ minh họa

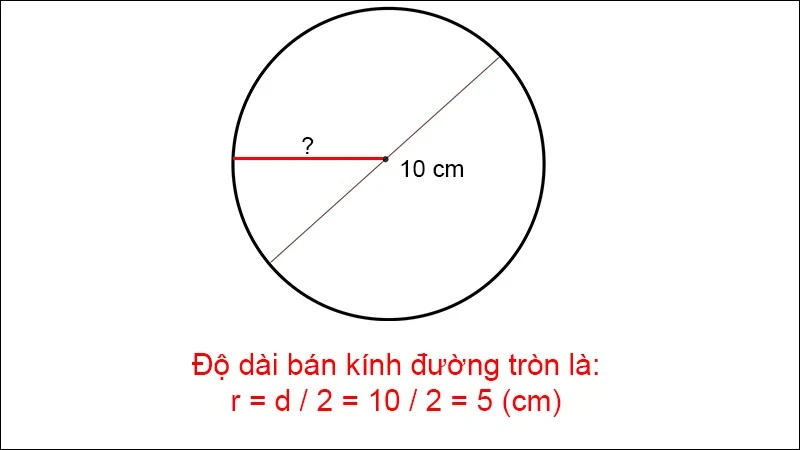
Giả sử đường kính của hình tròn là 10 cm. Như vậy, bạn sẽ tính bán kính như sau:

• Thay giá trị đường kính vào công thức:

\[ r = \frac{10}{2} = 5 \] Vậy bán kính của hình tròn là 5 cm.

Cách tính bán kính khi biết diện tích

Nếu bạn có diện tích của hình tròn, bạn cũng có thể tính bán kính dễ dàng chỉ bằng công thức sau:

Công thức

\[ r = \sqrt{\frac{S}{\pi}} \]

Ví dụ minh họa

Giả sử diện tích của hình tròn là 78.5 cm². Để tìm bán kính, bạn sẽ làm như sau:

• Thay giá trị diện tích vào công thức:

\[ r = \sqrt{\frac{78.5}{3.14}} \approx \sqrt{25} = 5 \] Vậy bán kính của hình tròn là 5 cm.

Một số bài toán thực tế về bán kính hình tròn

Bán kính hình tròn không chỉ là lý thuyết mà còn có ứng dụng rất lớn trong thực tế. Dưới đây là một số bài toán thực tế có thể gặp:

• Tính diện tích mặt nước của một hồ tròn: Nếu bạn biết được bán kính của hồ, bạn có thể dễ dàng tính diện tích để biết được khả năng chứa nước của hồ.
• Sản xuất vòng tròn: Khi thiết kế một sản phẩm hình tròn, việc xác định bán kính là rất quan trọng để đảm bảo tính chính xác và thẩm mỹ của sản phẩm.
• Xây dựng công trình: Bán kính cũng được sử dụng trong các lĩnh vực xây dựng, khi thiết kế các hình tròn như cột nhà, đài phun nước, hoặc các công trình nghệ thuật.

Kết luận

Như vậy, bán kính hình tròn là một khái niệm cơ bản nhưng vô cùng quan trọng trong toán học và thực tế. Từ việc xác định bán kính dựa vào chu vi, đường kính hay diện tích, bạn có thể áp dụng vào nhiều tình huống khác nhau. Hy vọng thông qua bài viết này, bạn đã có thêm kiến thức về cách tính bán kính hình tròn và ứng dụng của nó trong đời sống hàng ngày. Bằng cách hiểu rõ hơn về bán kính, bạn sẽ không chỉ nắm vững lý thuyết mà còn có thể ứng dụng nó một cách linh hoạt trong thực tế. Hãy cùng khám phá và áp dụng kiến thức này vào cuộc sống nhé!