Khám Phá Hình Hộp Chữ Nhật Và Cách Tính Diện Tích

Hình hộp chữ nhật là một trong những hình khối cơ bản và phổ biến trong toán học, đặc biệt là trong hình học. Với cấu trúc ba chiều, hình hộp chữ nhật có những ứng dụng rộng rãi trong đời sống hàng ngày, từ thiết kế kiến trúc đến đóng gói hàng hóa. Bài viết này sẽ giúp bạn tìm hiểu chi tiết về cách tính diện tích của hình hộp chữ nhật, bao gồm diện tích xung quanh và diện tích toàn phần, cùng với các ứng dụng thực tiễn.

1. Định Nghĩa Hình Hộp Chữ Nhật

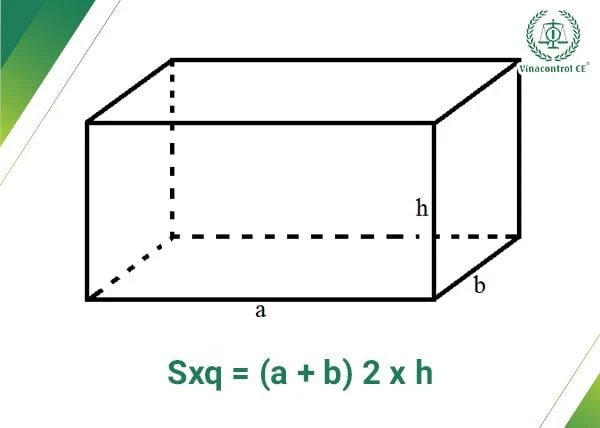
Hình hộp chữ nhật là một khối đa diện có sáu mặt, mỗi mặt đều là một hình chữ nhật. Hình hộp này được xác định bằng ba kích thước chính: chiều dài (a), chiều rộng (b), và chiều cao (h). Trong đó:

• Chiều dài (a): Là cạnh dài nhất của hình hộp.
• Chiều rộng (b): Là cạnh ngắn hơn chiều dài.
• Chiều cao (h): Là chiều cao từ mặt đáy đến mặt trên của hình hộp.

Hình hộp chữ nhật có một số đặc điểm nổi bật, như các mặt đối diện song song và bằng nhau, cũng như các góc đều bằng 90 độ.

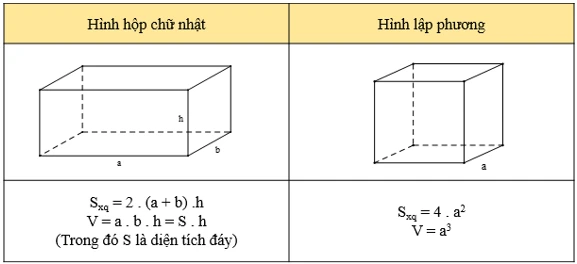
2. Công Thức Tính Diện Tích Xung Quanh

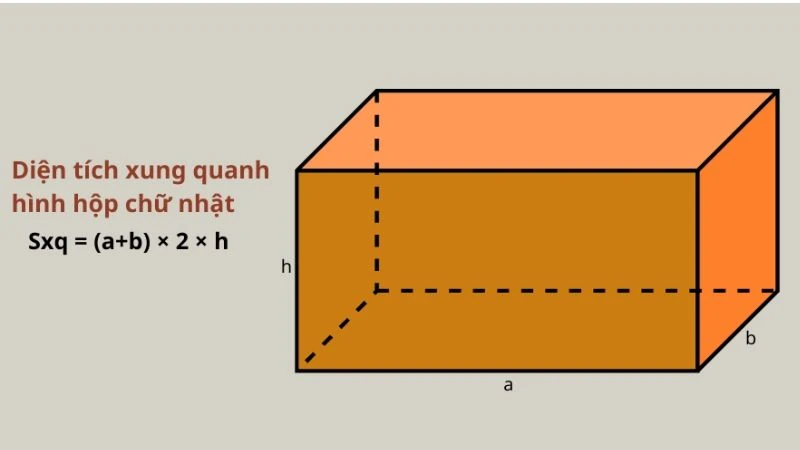
Diện tích xung quanh của hình hộp chữ nhật là tổng diện tích của bốn mặt xung quanh, không tính đến hai mặt đáy. Để tính diện tích xung quanh, bạn có thể sử dụng công thức sau: \[ S_{xq} = (a + b) \times 2 \times h \] Trong đó:

• \( S_{xq} \): Diện tích xung quanh.
• \( a \): Chiều dài.
• \( b \): Chiều rộng.
• \( h \): Chiều cao.

Lưu ý rằng tất cả các kích thước phải cùng đơn vị đo để có kết quả chính xác. Công thức này có thể hiểu là chu vi của đáy nhân với chiều cao. Ví dụ, nếu một hình hộp chữ nhật có chiều dài 4m, chiều rộng 3m và chiều cao 5m, diện tích xung quanh sẽ được tính như sau: \[ S_{xq} = (4 + 3) \times 2 \times 5 = 70 \, m^2 \]

3. Công Thức Tính Diện Tích Toàn Phần

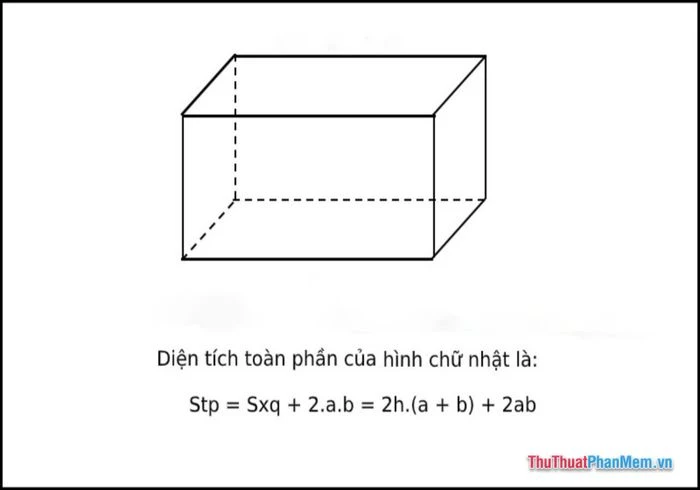
Diện tích toàn phần của hình hộp chữ nhật bao gồm diện tích xung quanh cộng với diện tích của hai mặt đáy. Công thức tính diện tích toàn phần được biểu diễn như sau: \[ S_{tp} = S_{xq} + 2 \times S_{đáy} \] Trong đó:

• \( S_{tp} \): Diện tích toàn phần.
• \( S_{đáy} \): Diện tích của một mặt đáy, được tính bằng công thức \( S_{đáy} = a \times b \).

Khi áp dụng vào ví dụ trước, diện tích đáy sẽ là: \[ S_{đáy} = 4 \times 3 = 12 \, m^2 \] Do đó, diện tích toàn phần sẽ là: \[ S_{tp} = 70 + 2 \times 12 = 94 \, m^2 \] Điều này có nghĩa rằng tổng diện tích bề mặt của hình hộp chữ nhật là 94 mét vuông.

4. Ứng Dụng Của Việc Tính Diện Tích Hình Hộp Chữ Nhật

Việc tính diện tích của hình hộp chữ nhật có nhiều ứng dụng thực tiễn trong cuộc sống:

4.1. Trong Kiến Trúc

Các kiến trúc sư thường sử dụng hình hộp chữ nhật để thiết kế các công trình xây dựng như nhà ở, văn phòng, hoặc các trung tâm thương mại. Việc tính toán chính xác diện tích giúp họ dự đoán được lượng vật liệu cần thiết và tối ưu hóa không gian sử dụng.

4.2. Trong Đóng Gói Hàng Hóa

Ngành logistics cũng rất chú trọng đến việc tính toán diện tích của các thùng hàng. Diện tích hình hộp chữ nhật giúp xác định không gian cần thiết để chứa và vận chuyển hàng hóa một cách hiệu quả.

4.3. Trong Giáo Dục

Trong giáo dục, việc giảng dạy về hình học, đặc biệt là hình hộp chữ nhật, giúp học sinh phát triển tư duy logic và khả năng tính toán. Các bài tập thực hành liên quan đến diện tích xung quanh và toàn phần góp phần củng cố kiến thức toán học cho học sinh.

Kết Luận

Tính diện tích hình hộp chữ nhật không chỉ là một phần kiến thức cơ bản trong toán học, mà còn là một kỹ năng thiết thực trong nhiều lĩnh vực khác nhau. Với các công thức tính đơn giản và dễ nhớ, bạn có thể nhanh chóng áp dụng vào các bài toán thực tiễn. Hãy nhớ rằng, việc nắm vững các khái niệm này sẽ giúp bạn không chỉ trong học tập mà còn trong công việc sau này. Nếu bạn có bất kỳ câu hỏi nào về cách tính diện tích hình hộp chữ nhật, đừng ngần ngại hỏi. Việc hiểu sâu về hình học sẽ mở ra cho bạn nhiều cơ hội trong tương lai. Hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích về hình hộp chữ nhật và cách tính diện tích của nó. Hãy áp dụng và thực hành để trở thành một chuyên gia trong lĩnh vực này!