Giới thiệu về Bán kính và Hình tròn

Khi nhắc đến các hình học cơ bản, hình tròn là một trong những hình dạng quen thuộc nhất. Nó xuất hiện xung quanh chúng ta trong cuộc sống hàng ngày, từ các bánh xe, đĩa quay cho đến các biểu tượng và hình ảnh. Một trong những khái niệm quan trọng nhất liên quan đến hình tròn chính là bán kính. Để hiểu rõ hơn về bán kính và cách tính toán nó, chúng ta sẽ cùng nhau khám phá các công thức và quy trình thực hiện.

1. Định nghĩa và Các Khái Niệm Cơ Bản

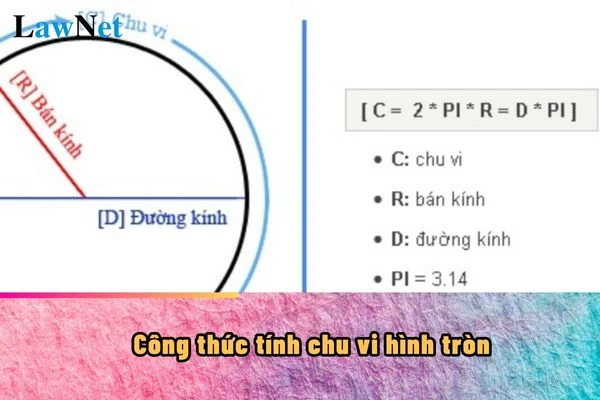
Hình tròn được định nghĩa là tập hợp tất cả các điểm trong mặt phẳng có khoảng cách bằng từ một điểm cố định gọi là tâm O. Khoảng cách đó được gọi là bán kính (r). Điểm xa nhất trên hình tròn từ tâm chính là đường kính (d), và mối quan hệ giữa bán kính và đường kính được thể hiện qua công thức: \[ d = 2r \] Từ công thức này, chúng ta có thể dễ dàng tính bán kính nếu biết đường kính: \[ r = \frac{d}{2} \] Ngoài ra, hình tròn còn có một đặc điểm quan trọng khác là chu vi (C), được tính theo công thức: \[ C = 2\pi r \] Trong đó, π (pi) là một hằng số có giá trị xấp xỉ bằng 3.14. Chu vi là độ dài của đường tròn, và nó có thể được sử dụng để tính toán bán kính nếu chúng ta biết giá trị của chu vi.

2. Cách Tính Bán Kính từ Chu Vi

Tính bán kính từ chu vi là một trong những bài toán đơn giản nhưng rất hữu ích. Để thực hiện, chúng ta làm theo các bước sau:

Bước 1: Ghi nhớ công thức

Như đã đề cập, chu vi của hình tròn được tính bằng công thức: \[ C = 2\pi r \]

Bước 2: Thay thế giá trị vào công thức

Giả sử bạn biết chu vi của một hình tròn là 31.4 cm. Để tìm bán kính, ta thế giá trị chu vi vào công thức: \[ 31.4 = 2\pi r \]

Bước 3: Giải phương trình

Chia cả hai vế cho \( 2\pi \): \[ r = \frac{31.4}{2\pi} \] Bây giờ, bạn có thể tính giá trị của bán kính: \[ r \approx \frac{31.4}{6.28} \approx 5 \text{ cm} \] Vậy bán kính của hình tròn này là 5 cm.

3. Tính Bán Kính từ Diện Tích

Ngoài chu vi, chúng ta cũng có thể tính bán kính từ diện tích của hình tròn. Diện tích (A) của hình tròn được tính bằng công thức: \[ A = \pi r^2 \] Nếu bạn biết diện tích, có thể sử dụng công thức sau để tìm bán kính: \[ r = \sqrt{\frac{A}{\pi}} \]

Ví dụ minh họa

Giả sử diện tích của hình tròn là 78.5 cm². Để tìm bán kính, bạn làm theo các bước như sau:

Bước 1: Thay thế giá trị vào công thức

\[ 78.5 = \pi r^2 \]

Bước 2: Giải phương trình

Chia cả hai vế cho π: \[ r^2 = \frac{78.5}{\pi} \] Tiếp theo, lấy căn bậc hai của cả hai vế: \[ r = \sqrt{\frac{78.5}{3.14}} \]

Bước 3: Tính giá trị

Sau khi tính toán, ta sẽ tìm được giá trị của bán kính: \[ r \approx \sqrt{25} \approx 5 \text{ cm} \] Như vậy, bán kính của hình tròn với diện tích 78.5 cm² là 5 cm.

4. Những Lưu Ý và Ứng Dụng Thực Tế

Khi thực hiện các phép tính liên quan đến bán kính hình tròn, có một số lưu ý bạn cần nhớ:

• Đơn vị đo: Khi tính toán, hãy chắc chắn rằng các đơn vị đo (cm, m, mm) là đồng nhất để tránh sai số.
• Hằng số π: Bạn có thể sử dụng giá trị xấp xỉ 3.14 hoặc 22/7 trong các phép tính, tùy theo độ chính xác yêu cầu.
• Ứng dụng thực tế: Bán kính không chỉ quan trọng trong toán học mà còn có ứng dụng trong kỹ thuật, kiến trúc, và nhiều lĩnh vực khác. Bạn sẽ thấy bán kính được sử dụng trong việc thiết kế bánh xe, các loại hình tròn trong công nghệ, và thậm chí trong thiên văn học.

Kết Luận

Bán kính là một khái niệm cơ bản nhưng vô cùng quan trọng trong hình học. Qua bài viết này, bạn đã nắm rõ cách tính bán kính từ chu vi và diện tích hình tròn, cũng như áp dụng được những kiến thức này vào thực tế. Việc hiểu rõ và vận dụng thành thạo các công thức này sẽ giúp bạn tự tin hơn trong việc giải quyết các bài toán liên quan đến hình tròn và bán kính. Chúc bạn thành công trong việc khám phá thế giới hình học!