Giới thiệu về hình chữ nhật

Hình chữ nhật là một trong những hình học cơ bản và phổ biến nhất trong toán học. Đây là một hình tứ giác có hai cặp cạnh song song và bằng nhau, đồng thời có bốn góc vuông. Hình chữ nhật không chỉ có mặt trong toán học mà còn xuất hiện trong rất nhiều lĩnh vực khác nhau như kiến trúc, thiết kế đồ họa, và thậm chí trong các ứng dụng hàng ngày như bảng, màn hình, hay cửa sổ.

Tính chất của hình chữ nhật

Hình chữ nhật có một số tính chất nổi bật mà bạn nên biết:

• Cạnh đối song song và bằng nhau: Nếu bạn có một hình chữ nhật với chiều dài là \( a \) và chiều rộng là \( b \), thì hai cạnh đối diện sẽ có chiều dài \( a \) và \( b \).
• Góc vuông: Tất cả bốn góc của hình chữ nhật đều là góc vuông (90 độ).
• Đường chéo: Hình chữ nhật có hai đường chéo, và chúng cắt nhau tại trung điểm. Độ dài của chúng bằng nhau và được tính từ các đỉnh đối diện.
• Diện tích và chu vi: Diện tích của hình chữ nhật được tính bằng công thức \( A = a \times b \), trong khi chu vi được tính bằng \( P = 2(a + b) \).

Công thức tính đường chéo

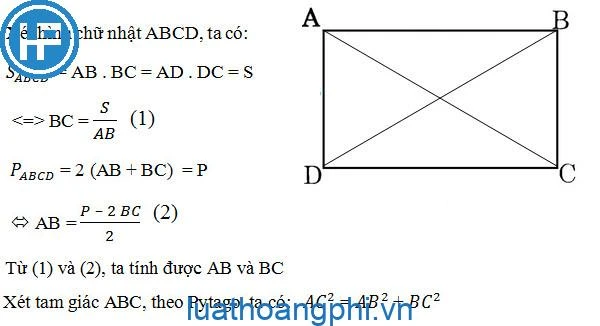
Để tính được độ dài của đường chéo hình chữ nhật, bạn cần sử dụng định lý Pytago. Đường chéo là cạnh huyền của một tam giác vuông, nơi hai cạnh còn lại là chiều dài và chiều rộng của hình chữ nhật.

Công thức

Công thức để tính độ dài đường chéo \( d \) của hình chữ nhật được biểu diễn như sau: \[ d = \sqrt{a^2 + b^2} \] Trong đó:

• \( d \) là độ dài đường chéo.
• \( a \) là chiều dài của hình chữ nhật.
• \( b \) là chiều rộng của hình chữ nhật.

Với công thức này, bạn có thể dễ dàng tính toán được độ dài đường chéo của bất kỳ hình chữ nhật nào chỉ cần biết chiều dài và chiều rộng của nó.

Ví dụ cụ thể về tính đường chéo

Để giúp bạn hiểu rõ hơn cách áp dụng công thức, hãy cùng xem qua một vài ví dụ cụ thể dưới đây.

Ví dụ 1

Giả sử bạn có một hình chữ nhật với chiều dài \( a = 4 \) cm và chiều rộng \( b = 3 \) cm. Để tính đường chéo \( d \), bạn có thể thay các giá trị vào công thức như sau: \[ d = \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5 \text{ cm} \]

Ví dụ 2

Trong một tình huống khác, nếu chiều dài của hình chữ nhật là \( a = 6 \) cm và chiều rộng là \( b = 8 \) cm, bạn có thể tính đường chéo như sau: \[ d = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \text{ cm} \]

Ví dụ 3

Hãy xem xét một hình chữ nhật có chiều dài \( a = 10 \) cm và chiều rộng \( b = 24 \) cm. Áp dụng công thức: \[ d = \sqrt{10^2 + 24^2} = \sqrt{100 + 576} = \sqrt{676} = 26 \text{ cm} \] Như vậy, bạn đã có thể tính được độ dài đường chéo của nhiều hình chữ nhật khác nhau. Các ví dụ này sẽ giúp bạn ghi nhớ công thức và áp dụng nó một cách nhanh chóng.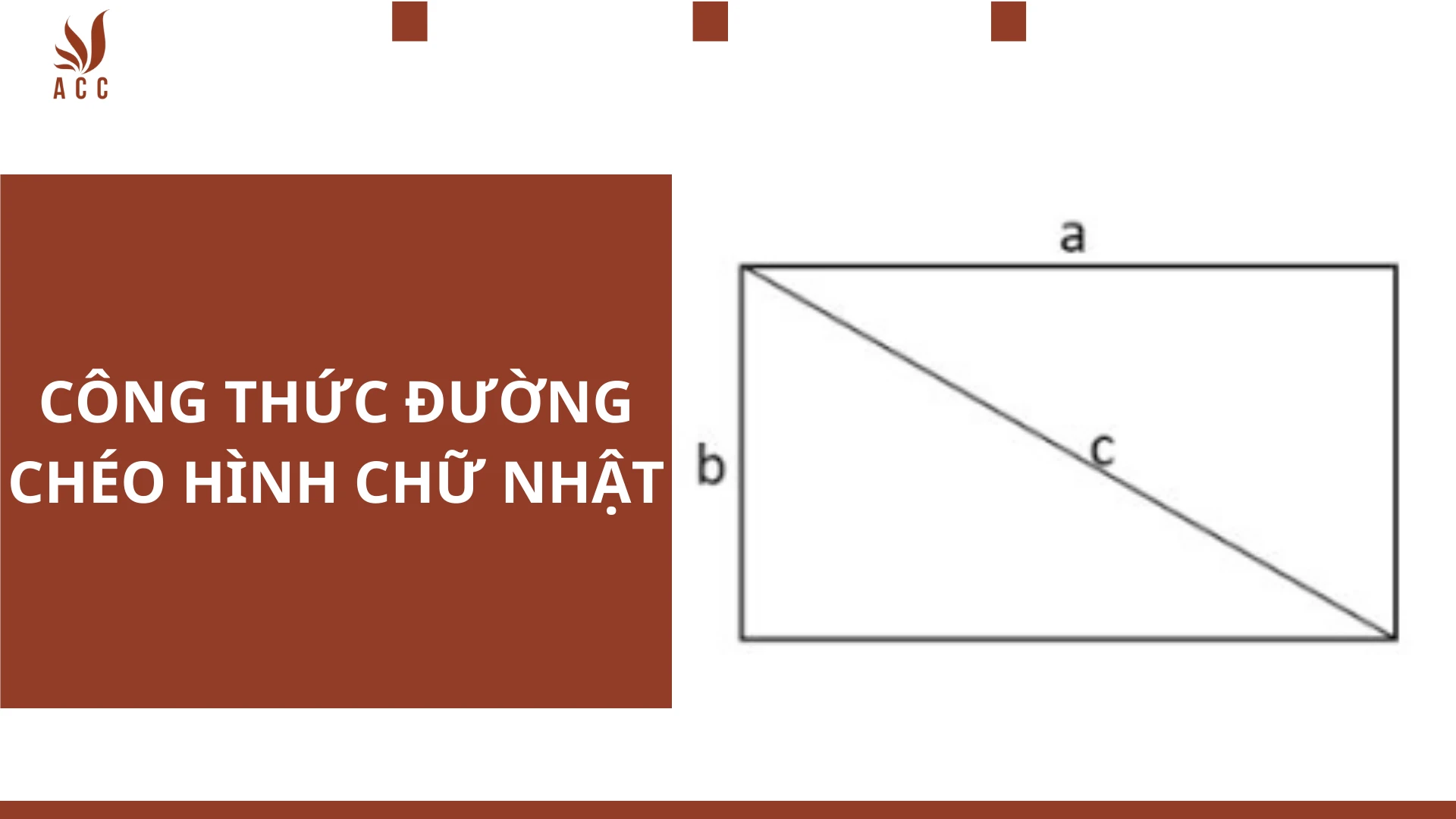

Ứng dụng của việc tính đường chéo hình chữ nhật

Việc tính đường chéo của hình chữ nhật không chỉ là một bài toán lý thuyết mà còn có rất nhiều ứng dụng thực tiễn trong cuộc sống hàng ngày. Dưới đây là một số lĩnh vực mà bạn có thể áp dụng kiến thức này.

Kiến trúc và xây dựng

Trong xây dựng, việc xác định kích thước của các thành phần như cửa, cửa sổ hay các bức tường là rất quan trọng. Đường chéo giúp các kỹ sư và kiến trúc sư đảm bảo rằng các thành phần này được lắp đặt chính xác và không bị lệch.

Thiết kế đồ họa

Trong thiết kế đồ họa, việc tạo ra các hình ảnh và layout thường yêu cầu tính toán các kích thước và vị trí. Đường chéo của hình chữ nhật giúp các nhà thiết kế đảm bảo rằng các yếu tố trong thiết kế được sắp xếp một cách hài hòa.

Đo đạc và không gian

Trong công việc đo đạc không gian, đường chéo của một khu vực có thể giúp bạn tối ưu hóa việc sắp xếp nội thất hoặc các thiết bị. Việc biết được độ dài đường chéo sẽ giúp bạn tận dụng tối đa không gian có sẵn.

Kết luận

Việc hiểu rõ về cách tính đường chéo của hình chữ nhật không chỉ giúp bạn giải quyết các bài toán trong sách giáo khoa mà còn mở ra nhiều cơ hội ứng dụng trong thực tế. Như bạn đã thấy, công thức tính rất đơn giản và dễ áp dụng, chỉ cần nhớ rằng đường chéo là cạnh huyền trong một tam giác vuông được tạo thành từ chiều dài và chiều rộng của hình chữ nhật. Hy vọng rằng qua bài viết này, bạn đã nắm rõ các khái niệm cũng như cách tính toán cần thiết để giải quyết những vấn đề liên quan đến hình chữ nhật. Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại hỏi để chúng ta cùng nhau khám phá thêm nhé!