
01/03/2025 20:30
Khám Phá Hình Lập Phương
Hình lập phương là một trong những hình khối phổ biến nhất trong toán học. Với sáu mặt đều là hình vuông, nó không chỉ đẹp mắt mà còn ứng dụng rộng rãi trong thực tế, từ kiến trúc, thiết kế nội thất cho đến các lĩnh vực khoa học kỹ thuật. Để hiểu rõ hơn về hình khối này, đặc biệt là các khía cạnh liên quan đến đường chéo của nó, chúng ta sẽ cùng nhau tìm hiểu sâu hơn trong bài viết này.Đặc Điểm Cơ Bản Của Hình Lập Phương
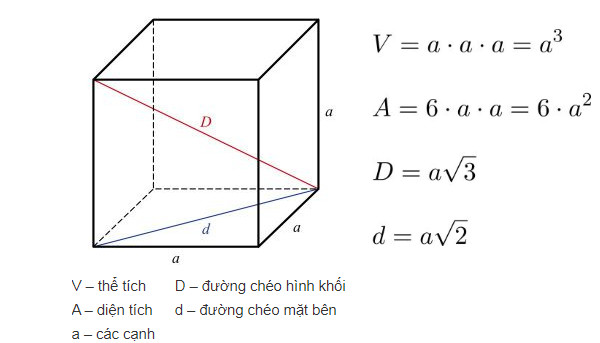
Trước khi đi vào chi tiết, chúng ta cần nắm rõ một số đặc điểm cơ bản của hình lập phương:- Cạnh (a): Độ dài của một cạnh của hình lập phương.
- Diện tích bề mặt: Tổng diện tích của tất cả các mặt của hình lập phương, được tính bằng công thức \( S = 6a^2 \).
- Thể tích: Tổng thể tích của hình lập phương, được tính bằng công thức \( V = a^3 \).
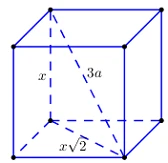
Đường Chéo Của Hình Lập Phương
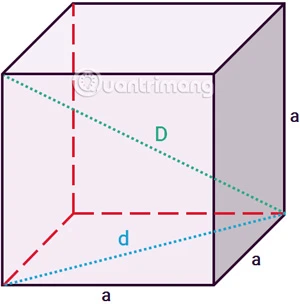
Đường chéo của hình lập phương là một trong những yếu tố thú vị và quan trọng trong hình học. Đường chéo không chỉ là một đoạn thẳng nối hai đỉnh đối diện nhau mà còn có thể được chia thành hai loại chính:- Đường chéo mặt (d): Là đoạn thẳng nối hai đỉnh đối diện trên cùng một mặt của hình lập phương.
- Đường chéo không gian (D): Là đoạn thẳng nối hai đỉnh đối diện trong không gian ba chiều.
Công Thức Tính Đường Chéo Mặt
Để tính chiều dài của đường chéo mặt, chúng ta áp dụng công thức sau: \[ d = a \sqrt{2} \] Trong đó:- \( d \) là độ dài của đường chéo mặt.
- \( a \) là độ dài cạnh của hình lập phương.
Công Thức Tính Đường Chéo Không Gian
Đường chéo không gian của hình lập phương được tính theo công thức: \[ D = a \sqrt{3} \] Trong đó:- \( D \) là độ dài của đường chéo không gian.
- \( a \) là độ dài cạnh của hình lập phương.

Ví Dụ Minh Họa
Để hiểu rõ hơn về cách tính độ dài đường chéo của hình lập phương, chúng ta sẽ xem xét một ví dụ cụ thể. Giả sử chúng ta có một hình lập phương có cạnh bằng 4 cm. Để tính độ dài đường chéo mặt và đường chéo không gian, chúng ta áp dụng các công thức đã nêu.- Tính đường chéo mặt:
- Tính đường chéo không gian:

Ứng Dụng Của Đường Chéo Trong Thực Tế
Đường chéo trong hình lập phương không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tế:- Kiến trúc: Các kiến trúc sư thường sử dụng hình lập phương và các đường chéo của nó để tính toán các yếu tố như độ vững chắc và tính thẩm mỹ trong thiết kế công trình.
- Khoa học vật liệu: Các nhà nghiên cứu trong lĩnh vực vật liệu thường tính toán các đặc tính của vật liệu dựa trên hình dạng hình học, bao gồm hình lập phương.
- Kỹ thuật: Trong các lĩnh vực như kỹ thuật điện tử và cơ khí, việc tính toán khoảng cách giữa các điểm trong không gian là rất quan trọng, và đường chéo hình lập phương giúp tối ưu hóa thiết kế.
Kết Luận
Hình lập phương là một trong những khối hình học đơn giản nhưng cũng rất thú vị. Việc tính toán độ dài của các đường chéo trong hình lập phương không chỉ đơn thuần là một bài toán học mà còn mang lại nhiều giá trị thực tiễn trong cuộc sống. Hy vọng rằng qua bài viết này, bạn đã có cái nhìn sâu sắc hơn về hình lập phương và những ứng dụng của nó trong thực tiễn. Nếu bạn có bất kỳ câu hỏi hay thắc mắc nào về hình lập phương hoặc các khái niệm liên quan, hãy để lại câu hỏi bên dưới để chúng ta cùng nhau thảo luận nhé!
Link nội dung: https://hoangnguyen.edu.vn/blog-a13843.html