Giới thiệu về hình ngũ giác

Hình ngũ giác là một trong những hình đa giác phổ biến, với năm cạnh và năm góc. Có hai loại ngũ giác: ngũ giác đều và ngũ giác không đều. Ngũ giác đều có đặc điểm là tất cả các cạnh và góc đều bằng nhau, trong khi ngũ giác không đều có các cạnh và góc khác nhau. Hình ngũ giác xuất hiện nhiều trong thực tế, từ kiến trúc đến nghệ thuật, và việc tính diện tích của nó là một trong những vấn đề quan trọng trong hình học.

Các loại hình ngũ giác

Ngũ giác đều

Ngũ giác đều là hình ngũ giác có năm cạnh bằng nhau và các góc bằng nhau. Mỗi góc trong ngũ giác đều có kích thước 108 độ. Để tính diện tích của ngũ giác đều, ta cần biết chiều dài cạnh (a) và sử dụng công thức sau: \[ \text{Diện tích} = \frac{5a^2}{4 \tan(\frac{\pi}{5})} \] Công thức này cho phép chúng ta tính diện tích một cách nhanh chóng và chính xác nếu biết chiều dài cạnh.

Ngũ giác không đều

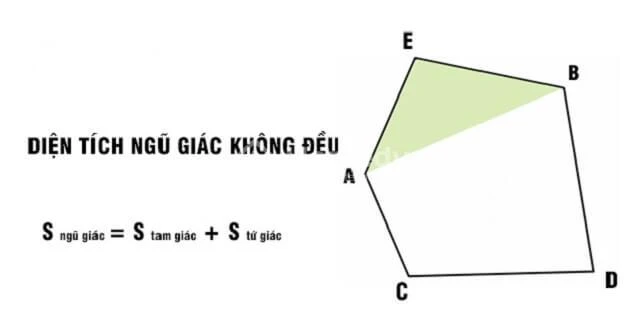
Ngược lại với ngũ giác đều, ngũ giác không đều có các cạnh và góc khác nhau. Việc tính diện tích của một ngũ giác không đều phức tạp hơn, thường yêu cầu biết chiều dài của tất cả các cạnh hoặc có thể chia ngũ giác thành các tam giác nhỏ hơn để tính diện tích. Một trong những phương pháp phổ biến để tính diện tích ngũ giác không đều là sử dụng công thức Heron hoặc chia ngũ giác thành nhiều hình tam giác.

Cách tính diện tích ngũ giác đều

Để tính diện tích của ngũ giác đều, ta cần thực hiện các bước sau:

• Xác định chiều dài cạnh (a): Đầu tiên, hãy đo chiều dài của một cạnh ngũ giác đều.
• Áp dụng công thức: Sử dụng công thức diện tích đã nêu ở trên.

Ví dụ, nếu chiều dài cạnh của ngũ giác đều là 6 cm, ta tính diện tích như sau: \[ \text{Diện tích} = \frac{5 \times 6^2}{4 \tan(\frac{\pi}{5})} = \frac{5 \times 36}{4 \tan(0.628)} \] Khi tính toán, ta có diện tích khoảng 61.62 cm².

Cách tính diện tích ngũ giác không đều

Để tính diện tích của một ngũ giác không đều, ta có thể áp dụng hai phương pháp chính:

Phương pháp chia thành tam giác

• Chia ngũ giác thành nhiều tam giác nhỏ: Vẽ các đường chéo từ một đỉnh đến các đỉnh còn lại của ngũ giác để tạo thành các tam giác.
• Tính diện tích từng tam giác: Sử dụng công thức tính diện tích tam giác, như công thức Heron hoặc công thức tính diện tích bằng chiều cao và cạnh đáy.
• Cộng diện tích các tam giác lại: Tổng hợp diện tích của tất cả các tam giác để ra diện tích tổng của ngũ giác.

Phương pháp Heron

Nếu biết độ dài của tất cả các cạnh của ngũ giác không đều, ta có thể sử dụng công thức Heron để tính diện tích.

• Tính chu vi (P):

\[ P = \frac{a + b + c + d + e}{2} \] Trong đó a, b, c, d, e là độ dài các cạnh của ngũ giác.

• Áp dụng công thức Heron:

\[ \text{Diện tích} = \sqrt{P(P-a)(P-b)(P-c)(P-d)(P-e)} \]

Ví dụ minh họa

Giả sử ta có một ngũ giác không đều với độ dài các cạnh là 4 cm, 5 cm, 6 cm, 7 cm và 8 cm. Đầu tiên, ta tính chu vi: \[ P = \frac{4 + 5 + 6 + 7 + 8}{2} = 15 \] Áp dụng công thức Heron để tính diện tích: \[ \text{Diện tích} = \sqrt{15(15-4)(15-5)(15-6)(15-7)(15-8)} = \sqrt{15 \times 11 \times 10 \times 9 \times 8 \times 7} \] Tính toán sẽ cho kết quả diện tích khoảng 89.47 cm².

Kết luận

Việc tính diện tích của hình ngũ giác, dù là ngũ giác đều hay không đều, là một quá trình thú vị và cần sự chú ý đến từng chi tiết. Với các công thức đơn giản và phương pháp rõ ràng, bạn có thể dễ dàng thực hiện các phép tính này một cách chính xác. Bằng cách hiểu rõ các khái niệm và áp dụng các công thức phù hợp, bất kỳ ai cũng có thể trở thành một "chuyên gia" trong việc tính toán diện tích của ngũ giác.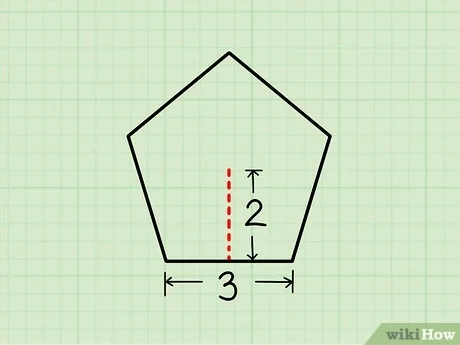 Hy vọng rằng bài viết này đã giúp bạn có thêm những kiến thức bổ ích về cách tính diện tích hình ngũ giác. Hãy áp dụng những kiến thức này vào thực tế và khám phá thêm nhiều điều thú vị từ toán học!